|
지구의 크기를 안다고 가정하고, 달의 크기를 구해보자.
지구의 크기를 모른다고 가정하면, 달의 크기가 지구에 비해 어느 정도 크기인지 비율을 구한다고 생각하면 된다.
1. 월식 이용한 달의 크기 계산
월식이 일어나는 날, 달에 비친 지구의 그림자를 보고 달의 크기를 대략 계산할 수 있다.
아래 그림은 월식사진에서 지구의 크기를 가늠하는 것으로써, 그림판에서 대충 그려본 것이다.

만일 지구의 직경이 13000km라 하면, 위와 같은 계산에 의하면 달의 직경은 13000/3.444 = 3775km가 된다(이렇게 된다는 걸 가정하는 것이며, 실제 달의 직경은 3,476km이다).
망원경이 발명되기 전이라도 달에 비친 지구의 그림자를 보고 대략 추정할 수 있었을 것이다.
망원경이 발명된 이후에는 더 정확히 추정할 수 있었을 것이다.
완전히 정확하지는 않더라도 달이 지구의 1/10인지 1/100인지 조차 모르는 것보다는 대략 1/3 정도라는 것만이라도 알게 된다는 건 큰 발견이 아닐 수 없다.
2. 보름달 이용한 달의 크기와 거리 계산
혜성의 출현이나 일식 등의 이벤트에 비해 월식이 훨씬 자주 일어나는 이벤트인 것은 분명하지만 이보다 더 자주 일어나는 이벤트를 이용하면 더 자주 측정할 수 있고 훈련에 의해 더 정확히 측정할 수 있을 것이다.
달의 시직경을 정확히 계산할 수 있으면 달의 크기와 달까지의 거리도 간단하게 계산할 수 있는 방법이 있다.
천문 관측기구 중 각도기 같은 것이 간의이다.

간의
간의의 정밀도가 어느 정도인지는 알 수 없지만, 만일 100분의 1도보다 더 정밀하게 측정할 수 있다면 달의 시직경을 이용하여 아래와 같이 계산하는 방법이 있다.
보름달이 뜬 맑은 날 저녁(18시)에 달의 시직경을 구한다. 이때, 0.51도라 가정하자.
그날 자정에 달의 시직경을 구한다. 이때, 0.52도라 가정하자.
이때, 시직경의 차이가 생기는 이유는 지구의 반경만큼 달에 가까워졌기 때문이다.
춘/추분날 적도에서 측정한 값이냐, 위도 35도에서 하지에 측정한 값이냐에 따라 아래 그림에서 말하는 r의 값은 차이가 나는데, 이는 당시 기술력으로 충분히 보정가능한 수준이라 가정한다.
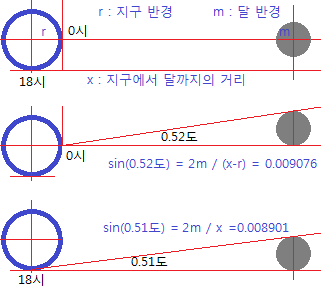
위 그림과 같은 경우, 18시 식과 0시 식을 연립하여 풀면 x = 51.863r임을 알 수 있다.
즉, 지구의 직경을 13000km라 하면,
x = 674,217km, m =3,000km임을 알 수 있다.
시직경 측정 정밀도를 높이면 오차 또한 줄일 수 있을 것이다.
또한, 달의 직경을 위 1번이나 혹은 다른 방법으로 보다 정밀하게 계산했을 경우, 위 2번식의 18시에 측정한 달의 시직경을 이용하여 지구에서 달까지의 거리를 구할 수 있다.
지구에서 달까지의 거리 = 달의 직경 / sin(달의 시직경) = 2m / sin(0.51도)
달의 시직경은 달의 남극에서 북극을 잇는 방향으로 재야한다. 왜냐하면 달의 적도 방향으로는 크기가 조금씩이나마 계속 변하기 때문이다. 즉, 18시에 동쪽의 달은 가로 방향으로 재야하고, 24시에 남쪽의 달은 세로 방향으로 재야 한다.
이런 방식으로 할 때 꼭 보름달이 아니어도 된다. 예를들어 반달이라도 된다. 하지만, 보름달일 때 가장 재기 쉽고 오차가 적지 않을까 싶다.
참고로, 현재는 지구에서 달까지의 거리를 주기적으로 엄청 정밀하게 재고 있다.
아폴로 달탐사 프로젝트시 달에 레이저 반사경을 설치해두었기 때문이다.
|