4색 문제에 대하여

 도는 지구
지구는 둥글고 나라 수는 유한하다

1. 4색문제

[참고 문헌]

4색 문제의 발견

1852년 10월, 영국 런던에 있는 유니버시티 대학(University College)의 대학원생 프랜시스 구트리에(Francis Guthrie)는 영국 지도를 색칠해 나가다가 '인접한 구획들이 같은 색으로 칠해지는 경우가 없게 하려면 최소한 몇 가지의 색이 필요할까?' 의문을 갖게 되었다.
결국 영국의 지도에 있는 지역들을 구별하여 색칠하는데는 4가지 색이면 충분하다는 사실을 알게 되었다.
그는 임의의 구획으로 나뉘어져 있는 지도를 칠할 때 네 가지 색이면 대부분 되는 것 같았지만 확신을 가질 수 없었다. 다섯 가지 이상의 색을 사용해야 조건에 맞게 그릴 수 있는 지도가 존재할까, 아니면 네 가지 색이면 어떤 지도에서도 인접한 구획들이 다른 색으로 칠해질 수 있음을 증명할 수 있을까?

문제 제기

구트리에는 런던대학의 학생이었던 남동생 프레더릭한테 물었고, 프레더릭은 다시 스승인 모르간(Augustus De Morgan)에게 물었다. 모르간은 또 아일랜드의 수학자이자 위대한 물리학자였던 해밀턴(William Rowan Hamilton)에게 편지를 썼다. 해밀턴도 다섯 종류의 색이 필요한 도형을 찾지 못했으며, 그런 도형이 존재하지 않는다는 것을 수학적으로 증명할 수도 없었다.
그 뒤 이 문제는 빠른 속도로 유럽에 전파되어 여러 사람들의 도전을 받았지만, 내로라하는 수학자들도 증명하지 못했고, 1878년 케일리(F.Cayley)에 의해 공식적으로 제기되었다.

유럽지도
유럽 지도

부족한 증명들

4색문제(four color problem)로 불리는 이 문제는 1879년 영국의 켐페(Alfred Bray Kempe)에 의해 풀렸다. 그렇게 알고 있었다.
그러다가 1890년, 더럼 대학의 강사였던 존 히우드(Percy John Heawood)는 켐페가 해결한 것으로 알려진 논문에서 오류를 발견했고, 이를 수정하여 다섯 종류의 색으로는 모든 지도를 칠할 수 있다는 결론을 내렸다.
이런 연구과정에서 위상수학(topology)라는 새로운 분야의 수학을 크게 발전시켰다.
1922년, 필립 프랭클린(Philip Franklin)은 25개 이하의 구획의 도형은 네 개 이하의 색으로 칠할 수 있음을 증명하였다.
1926년, 레이놀드(Reynolds)는 27개 구획으로 증명의 대상을 늘리는데 성공했다.
1940년, 빈(Winn)은 35개 구획, 1970년, 오르(Ore)와 스템플(Stemple)은 39개 구획으로까지 증명했다.
하지만, 이런 식의 방법으론 무한히 많은 구획을 다룰 순 없을 것이다.

새로운 기술

1976년, 미국 일리노이 대학의 볼프강 하켄(Wolfgang Haken)과 케네스 아펠(Kenneth Appel)은 새로운 테크닉을 개발했다.
그들은 '유한한 구획으로 나뉘어져 있는 유한한 개수의 지도들로부터 무한히 많은 구획으로 나뉘어진 무한개의 지도들을 유추해 낼 수 있다' 고 주장했던 하인리히 히쉬(Heinrich Heesch)의 업적을 줄곧 연구해 왔었다. 히쉬는 유한한 개수의 지도만으로 일반적인 경우를 다룰 수 있는 방법을 개발해 냈었다.
하켄과 아펠은 4색 문제를 히쉬의 아이디어로 단순화시키긴 했지만 그들이 얻은 결과는 '무한히 많은 모든 지도들이 4색으로 칠해질 수 있음을 증명하려면 1,482가지의 유한한 지도들만 고려하면 된다' 는 것이었다. 즉, 1482가지의 지도들이 모두 네 가지 색으로 칠해질 수 있음을 증명한다면 그것은 곧 모든 종류의 지도에 대해서도 성립한다는 결론이었다.

컴퓨터를 이용한 증명

이를 증명하려면 대형 컴퓨터를 이용해도 100년 동안은 돌려야 될 정도의 문제였다. 그러나 하켄과 아펠은 이에 대한 알고리즘을 연구(불필요한 부분은 계산하지 않게 하는 등의 연구)하여 1976년 6월, 1,200시간 동안 컴퓨터를 돌려 이를 증명했다.

발표된 증명은 본문과 도해를 담은 대략 50쪽과 2,500개의 또 다른 도해를 담은 85쪽 및 그 증명의 여러 부분에 대한 상세한 설명을 담은 400쪽의 마이크로피시(microfiche)와 함께 액면 그대로 받아들여야만 하는 계산 결과가 포함되어 있다.

아펠과 하켄의 증명은 완벽한 것으로 검증되었지만 지나치게 복잡하고, 기계의 힘을 빌렸으며, 이 문제의 증명 이외에는 쓸모가 전혀 없는 등의 이유로 수학자들을 그리 기쁘게 하지는 않았다.
이것은 우아하고 단순한 방법으로 증명되어야 할 문제로 여전히 남아 있다.

문제의 확장

지도 채색 문제는 자연스럽게 평면이 아닌 곡면 위에 그려진 지도로 확장되었다.
19세기로 접어들 때 히우드는 한 가지 경우를 제외할 때 임의의 닫힌 구면 위의 지도를 채색하는데 필요한 색의 최소 가짓수를 주는 것으로 보이는 공식을 발견했다.
오일러 표수가 n인 닫힌 곡면에 대해 그 공식은 색의 최소 가짓수가 다음과 같다고 예측한다.


예를 들면, n=0인 원환면 위의 임의의 지도를 채색하는데 필요한 색의 최소 가짓수는 7이고 n=2인 구면에 대해서 이 공식은 답 4를 제시한다.
(참고로 히우드에게는 이 공식이 구면의 경우에 정확한 답을 주는지를 증명할 수 없었고, 이에 따라 4색추측을 증명하는데 이 공식은 그에게 도움이 되지 못했다.)
히우드의 공식은 클라인 병을 제외한 모든 경우에 필요한 색의 최소 가짓수를 정확하게 제시함이 현재 분명하게 밝혀졌다. 클라인 병은 원환면과 같이 오일러 표수가 0이므로, 이 공식에 의해 일곱가지 색이면 충분하다. 그러나 클라인 병 위의 임의의 지도를 여섯 가지 색을 사용해서 채색할 수 있다.

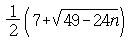
2. 태식의 4색 문제

세계지도
도입

필자(본 홈페이지의 개설자)는 이 문제를 1990년(고 3때)에 포항공대에서 어느 교수님으로부터 처음 듣게 되었다. 컴퓨터로는 증명이 되었는데 손으로는 증명되지 않은 문제라니 호기심이 발동하지 않을 리가 없잖은가. 언젠가 누군가의 손으로 멋지게 증명되길 기대해 보며 4색 문제와 비슷한 몇 가지 생각들을 여기에 쓰고자 한다.

4색 문제와 같다고?

문제

지구의를 칠하는 문제에서 규칙은 다음과 같다.

  1. 하얀 지구의가 있는데, 각 나라에 대한 경계선만 그려져 있다.
  2. 어떤 두 나라도 겹쳐지지 않고 경계가 명확하게 지구의에 그려져 있다.
    예를 들어, 공중이나 땅, 바닷속에서 여러 나라가 입체적으로 겹쳐지지 않는다.
    (지구의를 매끄러운 구형으로 보아도 무방하다.)
  3. 어느 나라도 흰색으로 칠해서는 안 된다.
  4. 같은 나라는 반드시 같은 색으로 칠해야 한다.
  5. 선으로 인접한 나라는 서로 다른 색으로 칠해야 한다.
  6. 한 점에서 여러 나라가 인접한 경우, 선으로 인접하지 않는 나라는 같은 색을 칠해도 상관이 없다.
이 때, 최소의 색으로 지구의를 칠하려 하면 몇가지의 색이 필요한가?

문제의 의도는?

위 문제는 4색 문제와 비슷해 보이지만 많이 다르다.
만일 모든 나라를 4색만으로 칠할 수 있다면 사실은 5색이 든 셈이다. 왜냐하면 어떤 나라도 아닌 땅은 흰 색이 칠해져 있기 때문이다. 만일 모든 나라를 4색으로 칠할 수 있고, 나라에 속한 땅도 흰 색으로 칠해도 된다면 이는 4색만으로 해결할 수 있다. 결국, 임자(나라)없는 땅도 하나의 나라로 보면 되는 것이다. 그러나 세계지도를 그릴 때, 어느 나라가 자기 나라의 색을 바다와 같게 칠해지길 바랄 것인가? 만일 일본을 바다와 같은 색으로 표시한다면 일본은 지도에 없거나 검은 선만 나오는 투명국이 될 것이다.

원래 4색문제는 구획을 나누고 색을 칠하는 문제이다. 위 문제에선 나라를 구획으로 삼고 있다. 그것까지는 좋다. 근데 같은 나라는 반드시 같은 색으로 칠하라고 한다. 만일 모든 나라는 한 덩어리로 되어 있다면 이는 또한 4색문제와 같다. 그러나 실제, 한 덩어리로만 된 나라가 어디 있단 말인가? 섬이 수천 개씩 되는 나라도 있는데 말이다. 그것도 좋다. 수천 개의 섬이 있어도 나라를 섬으로 일일이 구획을 나누지 않고 바다에서 경계를 만든다면 덩어리는 훨씬 줄어들 테니까 말이다. 그렇다고 해도 캐나다를 포위하고 있는 아래쪽 미국과 알래스카를 한 덩어리로 하긴 그렇지 않은가? 이런 경우는 어쩔 수 없이 두 덩어리가 되어야 할 것이다.

실제 현재 세계지도가 아닌 우리가 상상해서 만들 수 있는 모든 경우에 대해 최소의 색으로 지구의를 칠하는 게 위 문제의 의도이다. 그렇다면 대한민국의 일부가 미국, 영국과 접해있는 경우도 생각해야 하고, 심지어 미국과 캐나다 사이에 한국 땅이, 그 속에 또 미국 땅이, 그 속에 또 한국 땅이, ... 이렇게 유한번 반복되는 경우도 생각해야 할 것이다. 무한히 반복되는 것은 상상으로는 가능하지만 실제의 경우엔 존재할 수 없으니까 그냥 아주 큰 유한한 경우까지만 생각하자.

필자가 위 문제를 낸 의도는 결국 위 문제에선 4색만으론 칠할 수 없는 경우가 있음을 보여 주기 위함이다. 5색으로도, 6색으로도 부족한 경우가 있다. 이론상으로 만들 수 있는 얼마든지의 나라에 대해 그만큼의 색이 필요한 경우를 만들 수 있다.

필자는 여러분에게도 이 문제를 풀어볼 수 있는 즐거움을 주기 위해 잠시 이 페이지를 공사중으로 처리하고 싶다. 계속적인 많은 관심 부탁하며 이 페이지는 나중에 계속된다.

최초 작성일 : 1999.3.12