 차 례
차 례
| 사랑은 한순간의 열정이 아니다. 평생에 걸친 조용한 희생이다. |
|---|
 차 례
차 례
이 방법은 초기 상태(순서대로 수를 넣은 상태)에서 각 행의 합과 열의 합을 비교해 보고, 그 값을 같게 만드는 방법을 찾는 데서 착안되었다.
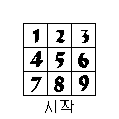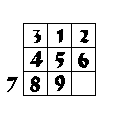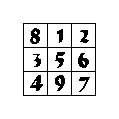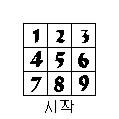
(1). 초기화
|
|||||||||||||||||||||||||||||||||||||||||||||||||||
(2). 1행 열이동
|
(3). 3행 열이동
|
||||||||||||||||||||||||||||||||||||||||||||||||||
(4). 1열 행이동
|
(5). 3열 행이동
|
||||||||||||||||||||||||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||||||||||||||||||||||
2.2. 대각선 진행 알고리즘에 의한 방법
(이 위치를 현위치, 현수를 1이라고 하자.)
현위치의 행이 첫 행이 아니라면 다음위치의 행은 그 위쪽 행이 된다.
현위치의 열이 마지막 열이 아니라면 다음위치의 열은 그 오른쪽 열이 된다.
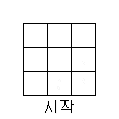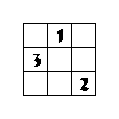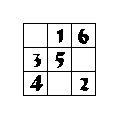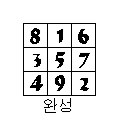
알고리즘에 의해 3차방진이 다음과 같이 만들어 진다. 이것은 또 대칭 및 회전에 의해 7가지의 방법이 더 있음을 알 수 있다.
(1)
|
(2)
|
(3)
|
|||||||||||||||||||||||||||
(4)
|
(5)
|
(6)
|
|||||||||||||||||||||||||||
(7)
|
(8)
|
(9)
|
|||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||
2.3. 대수적 방법
(1)
|
(1) 가장 가운데 수 e는 얼마일까?
아홉 개의 칸에 a부터 차례로 i까지 어떤 수가 들어간다. |
|||||||||
(2-1)
|
(2-1) 귀퉁이에 1이 있을 경우엔?
1이 있을 곳은 a와 b 둘 중 하나이다(대칭 및 회전에 의해 다른 곳도
같은 위치로 볼 수 있으므로). |
|||||||||
(2-2)
|
(2-2) 변에 1이 있을 경우엔?
여기서는 b가 1이라고 가정하자. |
|||||||||
(3)
|
(3) 하나의 해
이 해는 b=1이고 a=6일 경우의 해이다. |
또한 5차 이상의 홀수 방진에 대한 해의 총 개수(참고로 대칭 및 회전에 의해
달라질 수 있는 것을 하나로 칠 경우엔 3차방진의 해는 한 개이다)는 얼마나
될 것인가에 대해 연구해 보는 것도 좋은 일거리라 생각한다.
3. 5차 이상의 홀수 방진에 대하여
위에서 소개한 세 가지의 3차방진 해법을 완전히 이해했다면 5차 이상에
대해서도 해법을 구할 수 있다. 일반적으로 두번째에 소개한 대각선 진행
알고리즘은 너무 유명하여 대부분 알고 있으므로 5차 이상의 홀수 방진에
대해서 굳이 설명할 필요가 없으리라 본다. 다만 관심있는 사람은 아무리 큰
홀수 방진에 대해서도 이것이 성립함을 증명해 보라고 권하고 싶다.
4. 4차 방진은 쉽게
홀수 방진은 대각선 진행 알고리즘을 쓰면 모든 홀수 방진에 대해
가능함을 알게 되었다. 그렇다면 짝수 방진도 그렇게 쉽게 될까?
적어도 4차방진에 대해선 무척 쉬운 방법이 있음을 알 수 있다.
4.1. 행 및 열 교환에 의한 방법
(1). 초기화
|
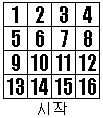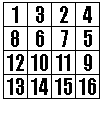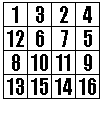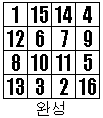
(1) 초기화
각 행 및 열의 합은 (1+2+...+16)/4)=34가 되어야 한다. |
||||||||||||||||||||||||||||||||||||
(2-1)
|
(2-1) 대칭 열교환 : 대각선 고정
대각선의 수들은 그대로 두자. |
||||||||||||||||||||||||||||||||||||
(2-2)
|
(2-2) 대칭 열교환 결과
그렇게 대칭교환시키니까 왼편과 같이 되었다. |
||||||||||||||||||||||||||||||||||||
(3-1)
|
(3-1) 대칭 행교환 : 대각선 고정
이제 마찬가지로 대칭 행교환을 한다. |
||||||||||||||||||||||||||||||||||||
(3-2)
|
(3-2) 대칭 행교환 결과
그러면 왼편과 같이 각 행의 합들도 같아졌음을 알 수 있다. |
||||||||||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||||||||
4.2. 행 및 열 교환법에 의한 4차방진의 예들
(1). 초기화
|
(1) 초기화 및 기호 설명
왼편과 같은 상태를 초기화 상태라 하자. |
||||||||||||||||||||||||||||||||||||
(2-1). 교환표
|
(2-2). 결과
|
||||||||||||||||||||||||||||||||||||
(3-1). 교환표
|
(3-2). 결과
|
||||||||||||||||||||||||||||||||||||
(4-1). 교환표
|
(4-2). 결과
|
||||||||||||||||||||||||||||||||||||
(5-1). 교환표
|
(5-2). 결과
결국 4차방진에선 위 4가지 방법이 대칭 및 회전에 의해 모두 같음을 알 수 있다. |
4차 방진은 두 행에 대해 열교환, 두 열에 대해 행교환 시켰었다.
(1-1). 교환표
|
(1-2). 결과
|
6차방진은 여덟 행 중 네 행에 대해 열교환, 여덟 열 중 네 열에 대해 행교환하는 방법을 찾으면 된다. 6차방진에서와 마찬가지로 8차방진에서도 대각선의 수들은 회전교환할 것이다. 그러면 나머지는 두 행에 대해서만 열교환, 두 열에 대해서만 행교환하는 방법을 찾는 문제로 간단해진다.
(1-1). 교환표
|
(1-2). 결과
|