| 최초의 컴퓨터는 파스칼의 계산기 |
|---|
1. 소개
n이 자연수일 때, (a+b)의 n 거듭제곱에 관한
이항전개식을 a에 대한 내림차순으로 쓰면 다음과 같은 형태가 될 것이다.
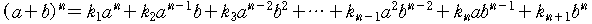
이 때, 각 항에 대한 계수(k1, k2, ...)를 어떻게 구할 것인가에 대해 생각해 보자.
2. 파스칼 삼각형
이항전개식의 각 항에 대한 계수(k1, k2, ...)를 구하는 쉬운
방법 중의 하나가 파스칼 삼각형을 이용하는 것이다.
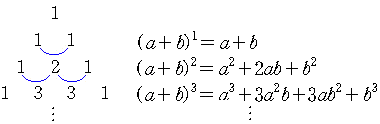
이는 n의 값이 작을 때 쉽고 유용하게 사용될 수 있다.
그러나, n의 값이 무척 클 때 언제까지 이렇게 계산할 것인가?
수학자들은 아무리 큰 n에 대해서도 곧바로 쉽게 딱 떨어지는 일반적인 방법을
요구할 것이다.
3. 이항전개식
이는 n개의 동전에 대해 앞면(a)을 i개, 뒷면(b)을 n-i개 뽑는 방법의 수를 찾는
문제로 생각할 수 있다.
결국 그 각각은 조합에 의해 계수를 구할 수 있으며, 그 전개식은 다음과 같다.
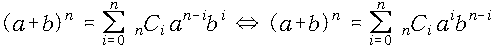
여기서 전개했을 때, a에 대한 내림차순으로 되는 것이 왼편의 식이고, a에 대한
오름차순으로 되는 것이 오른편의 식이며, 이 두 식은 동치이다(똑같다).
만일 어떤 책에서는 왼편처럼, 또 다른 책에서는 오른편처럼 되어 있다고 해서
출판사에 잘못되었다고 전화하는 일이 없도록 하자.
이처럼(혹은 이보다 훨씬 더) 똑같은 결과를 나타내는 식이 겉보기에 달라 보이는
경우가 있는데, 모범답안이라고 하는 것에 대해서도 일일이 확인해 봐야 하는 경우가
간혹 있다.
앞으로 나타나게 될 식에서는 편의상 위의 오른편 식처럼 a에 대한 오름차순으로 나타나는 식을 택할 것이다.
이제는 셋 이상의 항을 가진 다항전개식은 어떻게 되는지 알아보자.
3. 다항전개식
세 개의 항(a,b,c)을 가지는 전개식도 이항전개식과 별다를 게 없다.
a,b,c가 하나씩 들어 있는 n개의 주머니에서 적당히 n개(a를 i개, b를 j개,
c를 n-i-j개) 뽑는 방법의 수를 찾는 문제와 다를 바가 없기 때문이다.
결국 그 각각은 조합에 의해 계수를 구할 수 있고, 그 전개식은 이들을
적당히 중복되지 않게 더하도록 만들어 주면 되기 때문이다.
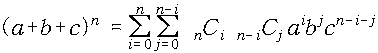
마찬가지 방법으로 m(일반적인 경우이므로 m이 2이상의 자연수이면 가능) 개의 항을 n번 거듭제곱했을 때 그 전개식은 다음과 같다.
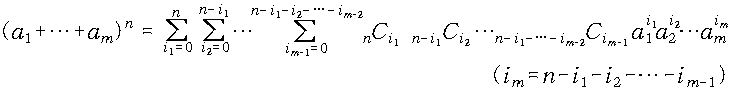
이제는 1999개의 항을 가지는 식을 1999회나 거듭제곱했을 때에도 각각의 항에 대한 계수를 구할 수 있겠지(내가 너무 오버했나)?