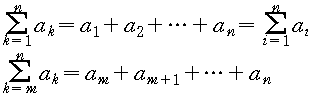거듭제곱의 합
남이 한다 하여 의(義) 아니면 좇지 말며, 남이 하지 않는다 하여 의(義)를 버리지 말라

1. 도입 배경

고등학교 때로 기억된다. 시그마 기호를 배웠을 때, 1부터 n까지 자연수의 합, 자연수의 제곱의 합, 세제곱의 합까지는 책에 나와 있었다. 또 그 증명은 수학적 귀납법을 쓰면 쉽게 해결되었다. 하지만 네제곱 이상의 합에 대해선 기술된 책을 못 봤기에 이를 연구했었다. 아직 일반적인 경우에 대한 가벼운 방법을 발견하진 못 했지만, 나름대로 연구했던 내용을 여기에 소개하고자 한다.

2. sigma 기호에 대한 약속

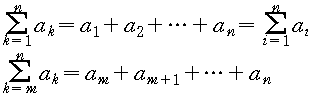sigma 식1 (식. 1)

위 식을 예로 들어 설명한다. 여기서 시그마를 sigma 라고 부르기로 하자. 첫번째 식에서 sigma 아래에 있는 'k=1'은 k의 초기값이 1이라는 의미이며, sigma 위에 있는 'n'은 k의 마지막 값이 n이라는 의미이다. 좌변의 식은 k값이 1부터 n까지 대응되는 a_k (아래첨자를 _ 로 표시) 에 대해 그 각 항들을 모두 더한다는 의미이다. 여기서 첨자가 된 k 대신에 i를 넣어도 마찬가지이다.
참고로 두번째 식에서처럼 sigma 아래에 'k=m'으로 되어 있으면 초항이 a_m이 된다는 의미이다.

3. 진태식의 유도법

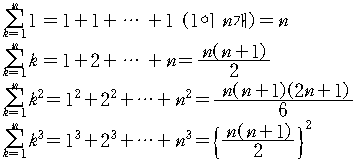sigma 식2 (식. 2)

위의 네 개의 식에 대한 증명은 수학적 귀납법을 이용하면 쉽게 해결할 수 있다. 하지만 필자는 그것을 다른 방법으로 접근하려 한다.
m 거듭제곱의 합까지 계산식을 알 때, m+1 거듭제곱의 합을 구할 수 있는 방법을 소개한다.

3.1. 방법의 발상

우선, 위 식(식.2)에서 첫번째 식을 생각해 보자. 수의 약속으로부터 1을 n개 합하면 n이 됨은 자명하다.
첫번째 식을 알 때 다음을 생각해 보자.

. 1열 2열3열 ...(n-1)열 n열 녹색 합
1행111 ...11 .
2행11 1...11 1
3행1 1 1...11 2
...... ...... ... ...... ...
n행111 ...11 n-1
(n+1)행111 ...11 n
황색 합12 3...n-1n .

위 표는 (n+1)행 * n열에 모두 1이 들어간 경우로써 전체 수의 합은 (n+1)*n이 된다. 또 이것은 '황색 부분의 수의 합 + 녹색 부분의 수의 합'과 같다. 여기서 황색 부분의 수의 합은 열단위로, 녹색 부분의 수의 합은 행단위로 계산하면 다음과 같다.
전체 수의 합 = n * (n+1)
황색 부분의 수의 합 = 1 + 2 + ... + n
녹색 부분의 수의 합 = 1 + 2 + ... + n
따라서, n(n+1) = 2(1+2+...+n) 즉,
1+2+...+n = n(n+1)/2 (식.2)의 두번째 식을 만들었다.

마찬가지로, 두번째 식을 알 때 다음을 생각해 보자.

. 1열 2열3열 ...(n-1)열 n열 녹색 합
1행123 ...n-1n .
2행12 3...n-1n 1
3행1 2 3...n-1n 1+2
...... ...... ... ...... ...
n행123 ...n-1n 1+2+...+(n-1)
(n+1)행123 ...n-1n 1+2+...+n
황색 합12*2 3*3...(n-1)*(n-1)n*n .

여기서,
전체 수의 합 = (n+1) * (1+2+...+n)
황색 부분의 수의 합 = 1 + 2*2 + ... + n*n
녹색 부분의 수의 합 = 1 + (1+2) + ... + (1+2+...+n)
따라서,

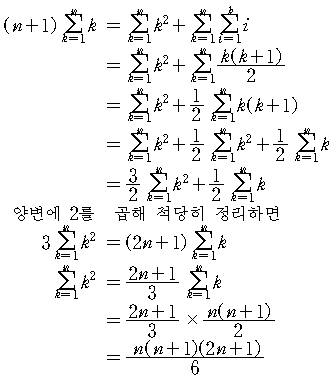sigma 식3 (식. 3)

이렇게 (식.2)의 세번째 식을 만들었다.

3.2. 일반적인 경우의 유도

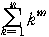마찬가지 방법으로, sigma k^m을 알 때, 다음과 같이 유도할 수 있다. 아래에서 'a^b'의 표기는 'a의 b 거듭제곱'의 의미이다.

. 1열 2열3열 ...(n-1)열 n열 녹색 합
1행1^m2^m 3^m...(n-1)^mn^m .
2행1^m2^m 3^m...(n-1)^mn^m 1^m
3행1^m 2^m 3^m...(n-1)^mn^m 1^m + 2^m
...... ...... ... ...... ...
n행1^m2^m3^m ...(n-1)^mn^m 1^m + ... + (n-1)^m
(n+1)행1^m2^m3^m ...(n-1)^mn^m 1^m + ... + n^m
황색 합1^m2 * 2^m 3 * 3^m...(n-1) * (n-1)^m n * n^m.

여기서,
전체 수의 합 = (n+1) * (1^m + 2^m + ... + n^m)
황색 부분의 수의 합 = 1*1^m + 2*2^m + 3*3^m + ... + n*n^m
= 1^(m+1) + 2^(m+1) + ... + n^(m+1)
녹색 부분의 수의 합 = 1^m + (1^m+2^m) + ... + (1^m+2^m+...n^m)
따라서,

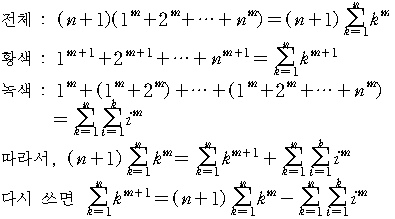sigma 식4 (식. 4)

위 식은 m = 0, 1, 2, ... 일 경우에 성립한다.

3.3. 식의 적용

위 식을 이용해 거듭제곱의 합에 관한 식을 다시 정리해 보자.

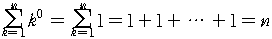sigma 식5 (식. 5)

지수가 0일 경우 위와 같이 된다. 이제 위 식과 (식.4)를 이용해 지수가 1일 경우 식이 어떻게 되는지 보자. 이 때, (식.4)의 식에서 m=0을 대입하여 다음과 같이 구할 수 있다.

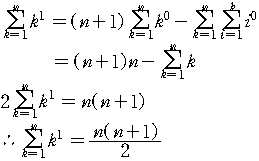sigma 식6 (식. 6)

마찬가지로 지수가 2일 경우를 알기 위해서 (식.4)에 m=1을 대입하고, (식.6)을 적당히 이용하여 다음과 같이 구할 수 있다.

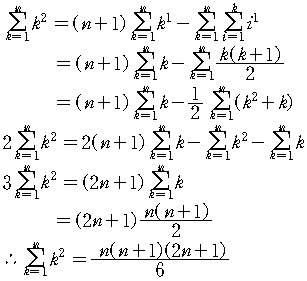sigma 식7 (식. 7)

마찬가지 방법으로 m=2,3,4,... 을 대입하고 적당한 이전 식을 이용하여 계속 지수가 k인 경우에 식을 구할 수 있다. 시간이 허락하는 한 이러한 방법으로 얼마든지 구할 수 있다. 아래에 그 결과식을 정리하여 표로 만들어 보았다.

3.4. 거듭제곱의 합에 관한 표

m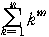
0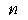
1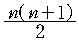
2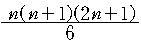
3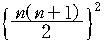
4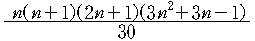
5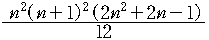
... ...

수학적 귀납법으로 이들을 증명해 보는 것도 재밌을 것이다.

3.5. 앞으로 과제

위 방식을 적당히 알고리즘화하여 식을 빨리 구하도록 하면 좋겠다.

최초 작성일 : 1998.3.